基础知识

动态规划问题的一般形式就是求最值。
求解动态规划的核心问题是穷举。
动态规划问题一定会具备最优子结构。
只有找到并列出正确的状态转移方程才能正确的穷举。
要符合最优子结构就需要子问题间必须相互独立。

斐波那契数列

常见方式为递归，代码如下：

function fib(n){
    if(n==1||n==2) return 1;
    return fib(n-1)+fib(n-2);
}

递归算法的时间复杂度等于子问题个数乘以解决一个子问题需要的时间。
- 其中：子问题个数就是递归树中节点的总数，二叉节点总数为制数级别，故为O(2^n)。
- 时间复杂度为制数级别十分费时。

重叠子问题

观察下面的递归树：可以发现存在大量的重复计算

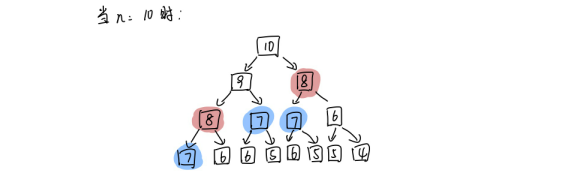
构建备忘录解决重叠子问题步骤：
1、构造备忘录（数组/字典）；
2、计算出子问题的答案先将其存储在备忘录中，再返回；
3、每次遇到一个子问题先去备忘录中查询，如果已存在答案直接使用。

function fib(n){
    if(n<1) return 0;
    let memo = new Array(n+1).fill(0);
    return helper(memo,n);
}
function helper(memo,n){
    if(n==1||n==2) return 1;
    if(memo[n]!=0) return memo[n];
    memo[n] = helper(memo,n-1)+helper(memo,n-2);
    return memo[n];
}

以下为具体过程：

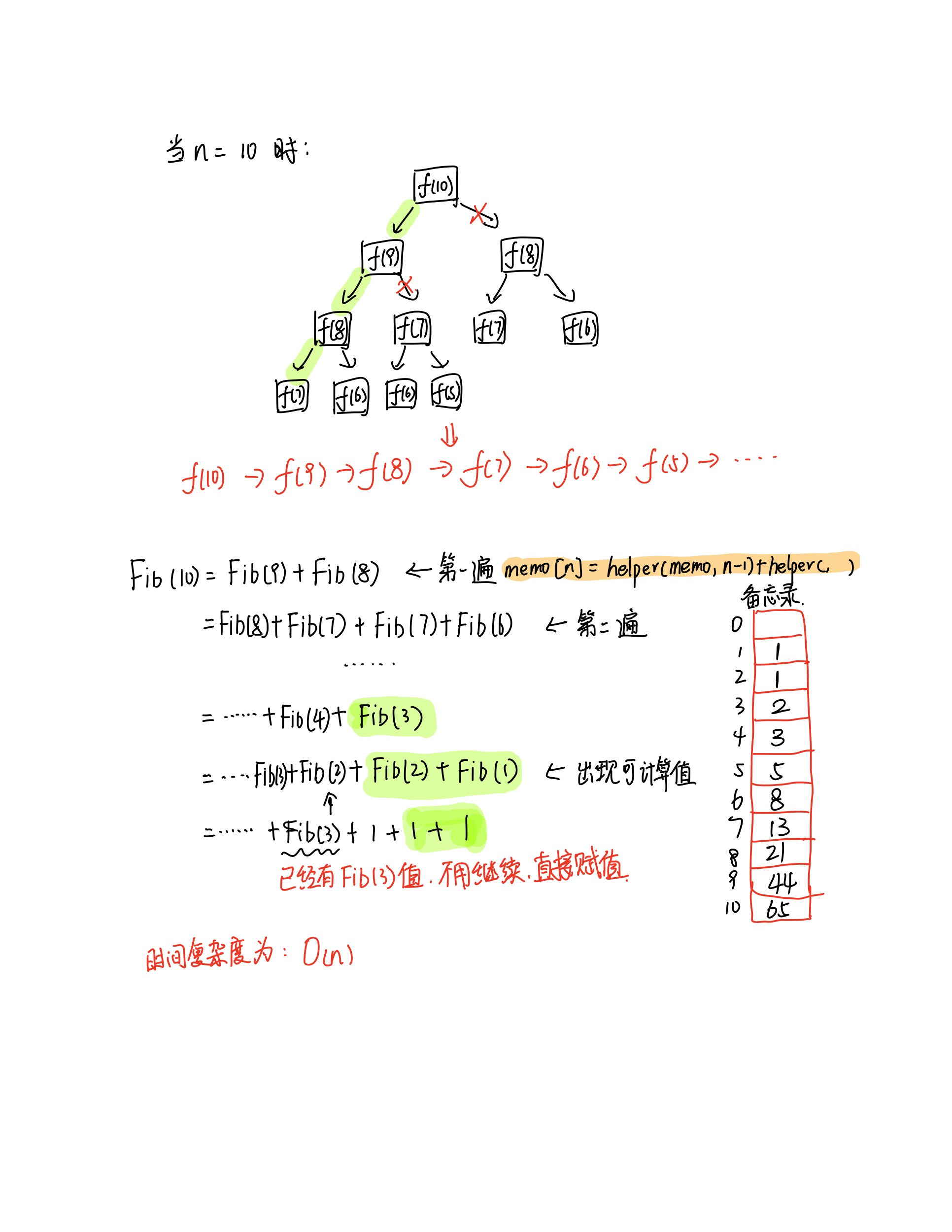
这种方法可以理解为自顶向下解法，而动态规划为自底向上解决问题。

自底向上的dp数组迭代解法

先看代码：

function fib(n){
    let dp = new Array(n+1).fill(0);
    dp[1]=dp[2]=1;
    for(let i=3;i<=n;i++){
        dp[i]=dp[i-1]+dp[i-2];
    }
    return dp[n];
}

代码更为简单，实际上就是在dp数组上进行操作，给定你需要求解的数值，直接计算到对应位置即可。

状态转移方程

状态转移方程实际上就是描述问题结构的数学形式，对于这个问题状态转移方程如下：

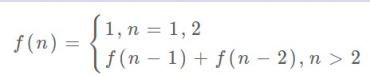
寻找状态转移方程是非常关键的一步。

列出状态转移方程步骤

1、确定状态；即原问题和子问题中的变化变量。
2、确定dp函数的定义。
3、确定选择并择优；即对于每个状态，可以做出什么选择改变当前状态。
4、最后明确base case。

代码优化

通过观察状态转移方程我们可以发现当前状态的数值只与当前状态的前两个状态有关，所以我们可以将空间复杂度进一步降低。代码如下：

function fib(n){
    if(n==1||n==2){
        return 1;
    }
    let prev=1,curr=1;
    for(let i=3;i<=n;i++){
        let sum = prev+curr;
        prev = curr;
        curr = sum;
    }
    return curr;
}